
No x intercept for the graph of function in part c).ġ) Go to the applet window and set the values of a, b and c for each of the examples in parts a, b and c above and check the discriminant and the x intercepts of the corresponding graphs.Ģ) Use the applet window to find any x intercepts for the following quadratic functions. The graph of function in part b) has one x intercept at (1,0). One repeated real solutions x_1 = -b / 2a = -2 / -2 = 1

The graph of function in part a) has two x intercepts are at the points (1,0) and (-3,0). The solutions are given by the quadratic formulasĮxample: Find the x intercepts for the graph of each function given below It has one repeated solution when D is equal to zero. The above equation has two real solutions and therefore the graph has x intercepts when the discriminant D = b 2 - 4 a c is positive. The x intercepts of the graph of a quadratic function f given byĪre the real solutions, if they exist, of the quadratic equation Check that the graph opens down ( a 0 ) and that the vertex is at the point (1,-1) and is a minimum point.Ĭ - x intercepts of the graph of a quadratic function H and k can also be found using the formulas for h and k obtained above.Ī) Go back to the applet window and set a to -2, b to 4 and c to 1 (values used in the above example). Group like terms and write in standard form We now divide the coefficient of x which is -2 by 2 and that gives -1. The x and y coordinates of the vertex are given by h and k respectively.Įxample: Write the quadratic function f given by f(x) = -2 x 2 + 4 x + 1 in standard form and find the vertex of the graph. When you graph a quadratic function, the graph will either have a maximum or a minimum point called the vertex. This is the standard form of a quadratic function with h = - b / 2a Let us start with the quadratic function in general form and complete the square to rewrite it in standard form.įactor coefficient a out of the terms in x 2 and xĪdd and subtract (b / 2a) 2 inside the parenthesesį(x) = a ( x 2 + (b/a) x + (b/2a) 2 - (b/2a) 2 ) + cį(x) = a ( x + (b / 2a) ) 2 - a(b / 2a) 2 + cį(x) = a ( x + (b / 2a) ) 2 - (b 2 / 4a) + c Where h and k are given in terms of coefficients a, b and c. You may change the values of coefficient a, b and c and observe the graphs obtained.Īnswers B - Standard form of a quadratic function and vertexĪny quadratic function can be written in the standard form Note that the graph corresponding to part a) is a parabola opening down since coefficient a is negative and the graph corresponding to part b) is a parabola opening up since coefficient a is positive. Use the boxes on the left panel of the applet window to set coefficients a, b and c to the values in the examples above, 'draw' and observe the graph obtained.

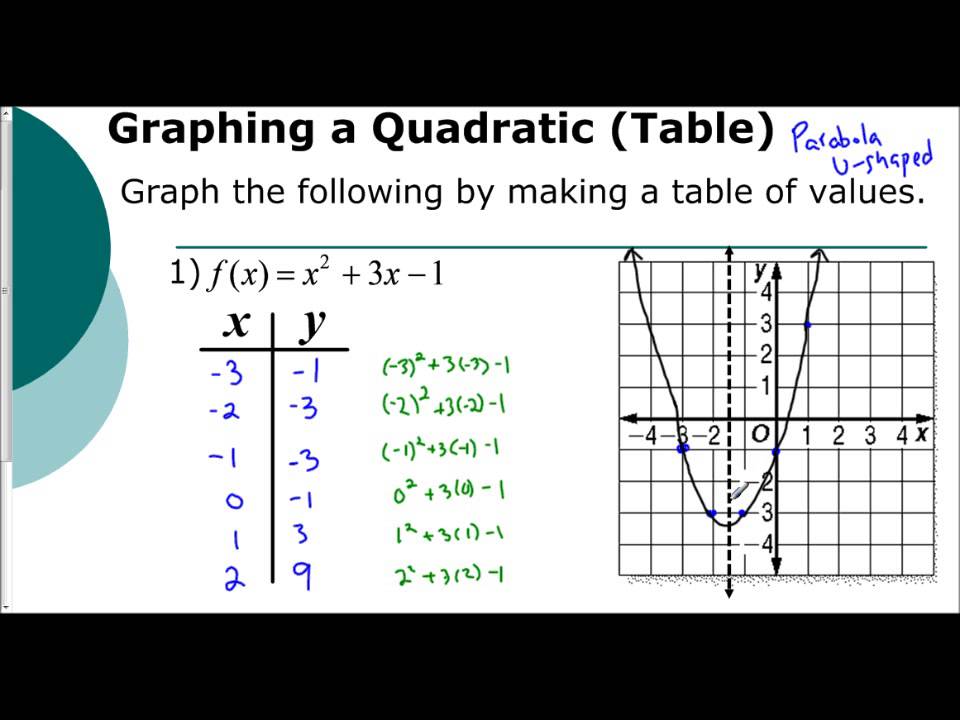
Įxplore quadratic functions interactively using an html5 applet shown below press "draw' button to start It is a "U" shaped curve that may open up or down depending on the sign of coefficient a. The graph of the quadratic function is called a parabola. Where a, b and c are real numbers and a not equal to zero. Once you finish the present tutorial, you may want to go through tutorials on quadratic functions, graphing quadratic functions and Solver to Analyze and Graph a Quadratic FunctionĪ quadratic function f is a function of the form The exploration is carried by changing values of 3 coefficients a, b and c included in the definition of f(x). You can also use this applet to explore the relationship between the x intercepts of the graph of a quadratic function f(x) and the solutions of the corresponding quadratic equation f(x) = 0. The properties of their graphs such as vertex and x and y intercepts are explored interactively using an html5 applet. Quadratic functions are some of the most important algebraic functions and they need to be thoroughly understood in any modern high school algebra course.


 0 kommentar(er)
0 kommentar(er)
